Descriptions

Static condensation is a technique used in the solution of partial differential equations (PDEs) to reduce the size of the system to be solved. In the context of the ngsolve example, it likely refers to the use of static condensation to reduce the size of the system of equations being solved by the solver in ngsolve, a finite element library for the solution of PDEs. In this technique, certain degrees of freedom (DOFs) are eliminated from the original system, resulting in a smaller system that can be solved more efficiently. The eliminated DOFs can be recovered later by a post-processing step.

Static condensation refers to the process of eliminating unknowns that are internal to elements from the global linear system. They are useful in standard methods and critical in methods like the HDG method. NGSolve automates static condensation across a variety of methods via a classification of degrees of freedom.

In this tutorial, you will learn

• how to turn on static condensation (eliminate_internal or condense),
• how to get the full solution from the condensed system using data members
  • harmonic_extension_trans
  • harmonic_extension
  • inner_solve,
• their relationship to a Schur complement factorization,
• types of degrees of freedom such as COUPLING_TYPE.LOCAL_DOF, and
• an automatic utility for solving via static condensation.

from ngsolve import *
from ngsolve.webgui import Draw
from netgen.geom2d import unit_square

mesh = Mesh(unit_square.GenerateMesh(maxh=0.4))

fes = H1(mesh, order=4, dirichlet='bottom|right')
u, v = fes.TnT()

The code you provided is setting up a finite element space for the solution of a partial differential equation on a square domain using the ngsolve library. It starts by creating a mesh of the square domain using the unit_square.GenerateMesh(maxh=0.4) function, which creates a mesh with a maximum element size of 0.4. The function H1(mesh, order=4, dirichlet='bottom|right') creates a finite element space of H1 elements with polynomial order 4 on the given mesh and with Dirichlet boundary conditions on the bottom and right boundary of the square.

The variables u and v are the trial and test functions respectively, which are used to set up the weak formulation of the PDE. The TnT() function creates a tuple of these trial and test functions and it is used to define the weak form of the PDE.

The code snippet you provided is setting up the finite element space, but it’s not solving any PDE yet. The next steps would involve defining the PDE, setting up the weak form of the PDE, and then solving the system of equations using an iterative solver.

Asking BilinearForm to condense

• The assembled matrix A= a.mat can be block partitioned into

A= \left( \begin{matrix}
A_{LL} & A_{LE} \\
A_{EL} & A_{EE}
 \end{matrix} \right)

where $L$ denotes the set of local (or internal) degrees of freedom and $E$ denotes the set of interface degrees of freedom.

• In our current example $E$ consists of edge and vertex dofs while $L$ consists of triangle dofs. (Note that in practice, $L$ and $E$ may not be ordered contiguously and $L$ need not appear before $E$, but such details are immaterial for our discussion here.)
• The condensed system is known as the Schur complement:

S=A_{EE} - A_{EL}A_{LL}^{-1}A_{LE}

• When eliminate_internal (or condense) is set to True in a, the statement a.Assemble actually assembles $S$.

a = BilinearForm(fes, condense=True)
a += grad(u) * grad(v) * dx
a.Assemble()

f = LinearForm(fes)
f += 1 * v * dx
f.Assemble()

u = GridFunction(fes)

The code you provided sets up the weak formulation of a Poisson equation. The Poisson equation is a second-order partial differential equation that describes the distribution of a scalar quantity, such as temperature or pressure, in a given region.

The first line creates a bilinear form a which is used to define the left-hand side of the Poisson equation. The BilinearForm function takes two arguments: the finite element space fes and condense=True, which enables the static condensation technique.

The next line defines the bilinear form with the term grad(u) * grad(v) * dx, which corresponds to the Laplacian operator and represents the left-hand side of the Poisson equation. The dx operator is an integration over the entire domain. Finally, the Assemble() function is called to assemble the bilinear form.

The next two lines define the right-hand side of the Poisson equation by creating a linear form f and adding the term 1 * v * dx to it, where 1 is a constant coefficient and v is the test function. This term corresponds to a source term in the Poisson equation. The Assemble() function is called to assemble the linear form.

Finally, the GridFunction(fes) creates a grid function u which will store the numerical solution of the Poisson equation.

Now, the next step would be to solve the system of equations using a solver, such as the CG or GMRES solver and use the solution to visualize the solution or post-processing.

A factorization of the inverse

NGSolve provides

• a.harmonic_extension_trans =

\left( \begin{matrix}
0 & 0 \\
 -A_{EL}A_{LL}^{-1} & 0
\end{matrix}  \right)

• a.harmonic_extension =

\left( \begin{matrix}
0 &  -A_{LL}^{-1}A_{EL} \\
0 & 0
\end{matrix}  \right)

• a.inner_solve =

\left( \begin{matrix}
A_{LL}^{-1} & 0 \\
0 & 0
\end{matrix}\right)

To solve

\left(
\begin{matrix}
A_{LL} & A_{LE} \\ 
A_{EL} & A_{EE}
\end{matrix}
\right)
\left(
\begin{matrix}
u_L \\ u_E
\end{matrix}
\right)
=
\left(
\begin{matrix}
f_L \\ f_E
\end{matrix}
\right)

we use a factorization of $A^{−1}$ that uses $S^{−1}$. Namely, we use the following identity:

\left(
\begin{matrix}
u_L \\ u_E
\end{matrix}
\right)
=
\left(
\begin{matrix}
I & -A_{LL}^{-1}A_{LE} \\ 
0 & I
\end{matrix}
\right)
\left(
\begin{matrix}
A_{LL}^{-1} & 0 \\
0 & S^{-1}
\end{matrix}
\right)

\underbrace{
\left(
\begin{matrix}
I & 0 \\
-A_{EL}A_{LL}^{-1} & I
\end{matrix}
\right)
\left(
\begin{matrix}
f_L \\ f_E
\end{matrix}
\right)}_{
\left(
\begin{matrix}
f_L' \\ f_E'
\end{matrix}
\right)
}

We implement this formula step by step, starting with the computation of $f_L’$ and $f_E’$.

Full solution from the condensed system

The following step implements

\left(
\begin{matrix}
f_L' \\ f_E'
\end{matrix}
\right)
=
\left(
\begin{matrix}
I & 0 \\ -A_{EL}A_{LL}^{-1} & I
\end{matrix}
\right)
\left(
\begin{matrix}
f_L \\ f_E
\end{matrix}
\right)

f.vec.data += a.harmonic_extension_trans * f.vec

The line of code you provided is modifying the right-hand side vector of the Poisson equation after it has been assembled. The harmonic_extension_trans attribute of the bilinear form a is a matrix that represents the transformation to be applied to the right-hand side vector in order to account for the degrees of freedom that were eliminated by the static condensation technique. The harmonic_extension_trans matrix is a product of the inverse of the mass matrix and the stiffness matrix.

By adding the product of a.harmonic_extension_trans * f.vec to the right-hand side vector f.vec.data, it is modifying the right-hand side vector to account for the effect of the eliminated degrees of freedom. This modification is necessary to obtain an accurate solution of the Poisson equation after using the static condensation technique.

It is also important to note that the harmonic extension step is performed only once, before the first solve, and is not required for any subsequent solves of the linear system, as long as the matrix remains unchanged.

The next step implements part of the next matrix application in the formula.

u.vec.data = a.mat.Inverse(freedofs=fes.FreeDofs(coupling=True)) * f.vec

The line of code you provided is solving the Poisson equation using the Inverse() method of the matrix a.mat. The Inverse() method computes the inverse of the matrix and returns it.

The argument freedofs=fes.FreeDofs(coupling=True) is passed to the Inverse() method, it means that the inverse is only computed for the degrees of freedom that are not constrained by boundary conditions. This is done because the static condensation technique eliminates certain degrees of freedom from the system, and these eliminated degrees of freedom are not present in the matrix a.mat, so they do not need to be considered when solving the system.

The solution of the Poisson equation is then obtained by multiplying the inverse of the matrix a.mat with the right-hand side vector f.vec. The result is stored in the u.vec.data which is the numerical solution of the Poisson equation.

It is also important to note that the inverse of the matrix is only calculated once, before the first solve, and it is not required for any subsequent solves of the linear system, as long as the matrix remains unchanged.

• Note:
  • Because a has condense set, the inverse a.mat.Inverse actually computes S−1.
  • Note that instead of the usual fes.FreeDofs(), we have used fes.FreeDofs(coupling=True) or simply fes.FreeDofs(True) to specify that only the degrees of freedom that are not local and not Dirichlet should participate in the inverse computations. (The underlying assumption is that Dirichlet dofs cannot be local dofs.)

Next, we compute

\left(
\begin{matrix}
u_L' \\ u_E
\end{matrix}
\right)
=
\left(
\begin{matrix}
0 \\ u_E
\end{matrix}
\right)
+
\left(
\begin{matrix}
A_{LL}^{-1} & 0 \\ 0 & 0 
\end{matrix}
\right)
\left(
\begin{matrix}
f_L' \\ f_E'
\end{matrix}
\right)

u.vec.data += a.inner_solve * f.vec

The line of code you provided is modifying the solution vector u.vec.data of the Poisson equation after it has been computed. The inner_solve attribute of the bilinear form a is a matrix that represents the correction to be applied to the solution vector in order to account for the degrees of freedom that were eliminated by the static condensation technique.

By adding the product of a.inner_solve * f.vec to the solution vector u.vec.data, it is modifying the solution vector to account for the effect of the eliminated degrees of freedom. This modification is necessary to obtain an accurate solution of the Poisson equation after using the static condensation technique.

It is also important to note that the inner_solve step is performed only once, after the first solve, and is not required for any subsequent solves of the linear system, as long as the matrix remains unchanged.

Finally,

\left(
\begin{matrix}
u_L' \\ u_E
\end{matrix}
\right)
=
\left(
\begin{matrix}
I & -A_{LL}^{-1}A_{LE}  \\ 0 & I
\end{matrix}
\right)
\left(
\begin{matrix}
u_L' \\ u_E'
\end{matrix}
\right)

u.vec.data += a.harmonic_extension * u.vec
Draw(u)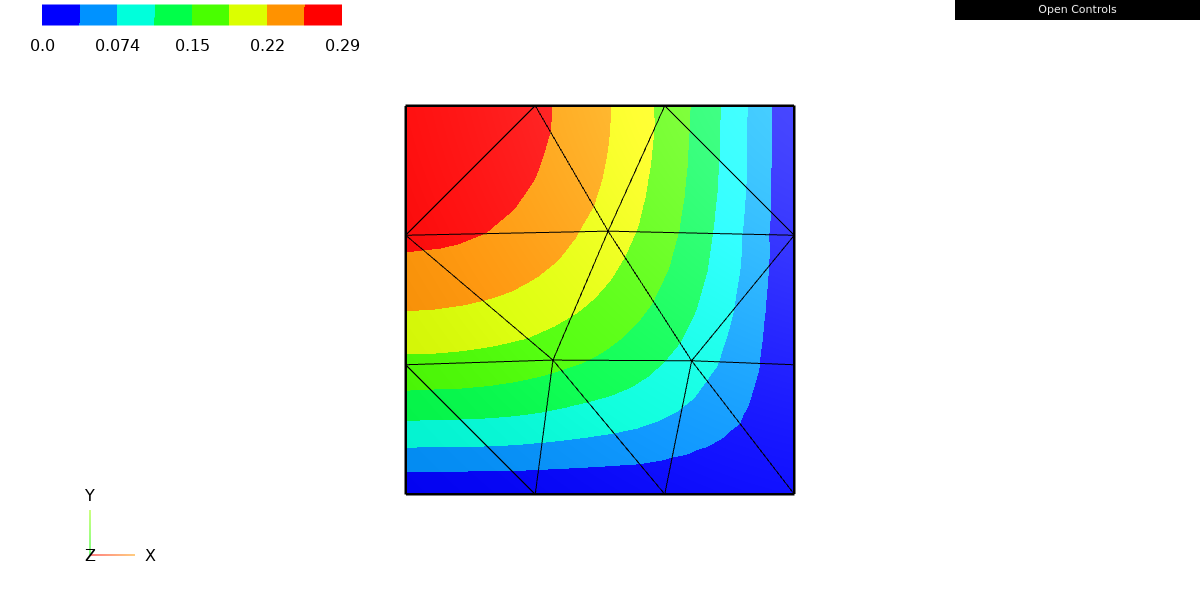

Beind the scenes: Coupling Type

How does NGSolve know what is in the index sets $L$ and $E$?

Look at ‘fes.CouplingType’ to see a classification of degrees of freedom(dofs).

for i in range(fes.ndof):
    print(fes.CouplingType(i))

dof_types = {}
for i in range(fes.ndof):
    ctype = fes.CouplingType(i)
    if ctype in dof_types.keys():
        dof_types[ctype] += 1
    else:
        dof_types[ctype] = 1
dof_types

#return 
{<COUPLING_TYPE.WIREBASKET_DOF: 8>: 15,
 <COUPLING_TYPE.INTERFACE_DOF: 4>: 90,
 <COUPLING_TYPE.LOCAL_DOF: 2>: 48}

The code you provided is printing the coupling type of all degrees of freedom (DOFs) in the finite element space fes. The fes.CouplingType(i) function returns the coupling type of the i-th degree of freedom, which can be one of the following:

• LOCAL_DOF: These are the degrees of freedom that are unique to a single element and are not shared with other elements. They are used to represent the local variations of the solution within an element.
• INTERFACE_DOF: These are the degrees of freedom that are shared between two or more elements, representing the continuity of the solution across element boundaries.
• WIREBASKET_DOF: These are the degrees of freedom that are used in the wirebasket method, which is a technique used to represent the solution in the vicinity of curved boundaries.

In general, the coupling type of a DOF determines how the DOF is connected to other DOFs in the system, and how it contributes to the solution of the PDE. LOCAL_DOF are used to represent local variations of the solution within an element, INTERFACE_DOF are used to maintain continuity across element boundaries, and WIREBASKET_DOF are used to represent the solution in the vicinity of curved boundaries.

By using the for loop, the script will iterate over all the degrees of freedom and print the corresponding coupling type.

This can be useful to understand the behavior of the static condensation technique and which degrees of freedom are eliminated.