Set up the bilinear form a(.,.) on the finite element space

Set up the bilinear form a(.,.) on the finite element space corresponding to the Laplacian operator -Delta, by adding the Diffusion domain integrator.

   BilinearForm a(&fespace);
   if (pa) { a.SetAssemblyLevel(AssemblyLevel::PARTIAL); }
   if (fa)
   {
      a.SetAssemblyLevel(AssemblyLevel::FULL);
      // Sort the matrix column indices when running on GPU or with OpenMP (i.e.
      // when Device::IsEnabled() returns true). This makes the results
      // bit-for-bit deterministic at the cost of somewhat longer run time.
      a.EnableSparseMatrixSorting(Device::IsEnabled());
   }
   a.AddDomainIntegrator(new DiffusionIntegrator(one));

This code is the same as I explained earlier, it creates a BilinearForm object, “a”, which is used to represent the left-hand side (LHS) of the linear system. The BilinearForm class is provided by the MFEM library, and it is used to represent bilinear forms in finite element spaces.

The BilinearForm object is created by passing a pointer to the finite element space, “fespace”, to its constructor.

The BilinearForm object “a” is then configured based on the values of the pa and fa variables. The pa variable is used to enable or disable partial assembly, and the fa variable is used to enable or disable full assembly.

Partial assembly is used to improve the performance of the assembly process by only assembling the non-zero entries of the matrix, rather than assembling the entire matrix. Full assembly is used to assemble the entire matrix. If the pa variable is set to true, the SetAssemblyLevel() method is called on the BilinearForm object, passing AssemblyLevel::PARTIAL as an argument, which enables partial assembly. If the fa variable is set to true, the SetAssemblyLevel() method is called on the BilinearForm object, passing AssemblyLevel::FULL as an argument, which enables full assembly.

The EnableSparseMatrixSorting() method is called on the BilinearForm object. This method sorts the matrix column indices when running on GPU or with OpenMP. This makes the results bit-for-bit deterministic at the cost of somewhat longer run time.

Finally, a DiffusionIntegrator object is created by passing the “one” ConstantCoefficient object to its constructor. The DiffusionIntegrator class is used to perform the integration of the bilinear form over a domain.

2. Assemble the bilinear form and the corresponding linear system

Assemble the bilinear form and the corresponding linear system, applying any necessary transformations such as: eliminating boundary conditions, applying conforming constraints for non-conforming AMR, static condensation, etc.

   a.Assemble();

   OperatorPtr A;
   Vector B, X;
   a.FormLinearSystem(ess_tdof_list, x, b, A, X, B);

   cout << "Size of linear system: " << A->Height() << endl;

This code assembles the bilinear form “a” and creates the linear system of equations. The static_cond variable is used to enable or disable static condensation, which is a technique that can be used to reduce the size of the linear system.

If the static_cond variable is set to true, the EnableStaticCondensation() method is called on the BilinearForm object “a”, which enables static condensation.

The Assemble() method is then called on the BilinearForm object “a”, which assembles the bilinear form, i.e., it computes the values of the bilinear form at the degrees of freedom of the finite element space.

A pointer to an Operator, “A”, is created, along with Vector objects “B” and “X”, which will be used to store the linear system of equations.

The FormLinearSystem() method is then called on the BilinearForm object “a”, passing the essential boundary true degrees of freedom list “ess_tdof_list”, the GridFunction “x”, the LinearForm “b”, the Operator “A”, the Vector “X”, and the Vector “B” as arguments. This method forms the linear system of equations by applying the boundary conditions and assembling the matrix and vector corresponding to the bilinear form.

The size of the linear system is obtained by calling the Height() method of the Operator “A”, which returns the number of rows in the matrix, and it is printed to the console.

In summary, this block of code assembles the bilinear form “a” and forms the linear system of equations. If static condensation is enabled, it applies it to the bilinear form. The linear system is then stored in the operator A, vector B and X. The size of the linear system is also printed to the console.

Solve the linear system $AX=B$

 if (!pa)
   {
#ifndef MFEM_USE_SUITESPARSE
      // Use a simple symmetric Gauss-Seidel preconditioner with PCG.
      GSSmoother M((SparseMatrix&)(*A));
      PCG(*A, M, B, X, 1, 200, 1e-12, 0.0);
#else
      // If MFEM was compiled with SuiteSparse, use UMFPACK to solve the system.
      UMFPackSolver umf_solver;
      umf_solver.Control[UMFPACK_ORDERING] = UMFPACK_ORDERING_METIS;
      umf_solver.SetOperator(*A);
      umf_solver.Mult(B, X);
#endif
   }
   else
   {
      if (UsesTensorBasis(fespace))
      {
         if (algebraic_ceed)
         {
            ceed::AlgebraicSolver M(a, ess_tdof_list);
            PCG(*A, M, B, X, 1, 400, 1e-12, 0.0);
         }
         else
         {
            OperatorJacobiSmoother M(a, ess_tdof_list);
            PCG(*A, M, B, X, 1, 400, 1e-12, 0.0);
         }
      }
      else
      {
         CG(*A, B, X, 1, 400, 1e-12, 0.0);
      }
   }

This code block solves the linear system of equations that was formed earlier. The solution is stored in the Vector “X”. The method used to solve the system depends on the value of the pa variable and the presence of SuiteSparse library.

If the pa variable is set to false, the system is solved using a simple symmetric Gauss-Seidel preconditioner with PCG. The GSSmoother class is used to create a smoother for the sparse matrix of the linear system, and the PCG method is used to solve the system. The PCG method takes the matrix “A”, smoother “M”, right-hand side “B”, and initial guess “X” as input. It also takes the maximum number of iterations, the tolerance, and the print level as input.

If the pa variable is set to true, then the system is solved using different methods depending on the type of finite element used (UsesTensorBasis) and whether the algebraic_ceed variable is true or false.

• If algebraic_ceed is true and the UsesTensorBasis is true, the system is solved using a Ceed algebraic solver. The ceed::AlgebraicSolver class is used to create a smoother for the sparse matrix of the linear system, and the PCG method is used to solve the system.
• If algebraic_ceed is false and the UsesTensorBasis is true, the system is solved using an OperatorJacobiSmoother class. The OperatorJacobiSmoother class is used to create a smoother for the sparse matrix of the linear system, and the PCG method is used to solve the system.
• If the UsesTensorBasis is false, the system is solved using CG method. The CG method takes the matrix “A”, right-hand side “B”, and initial guess “X” as input. It also takes the maximum number of iterations, the tolerance, and the print level as input.

If MFEM was compiled with SuiteSparse, the UMFPackSolver class is used to solve the system. The UMFPackSolver class is provided by SuiteSparse and it is used to solve sparse linear systems of equations using the UMFPACK library.

The UMFPackSolver object is created, and the Control[UMFPACK_ORDERING] is set to UMFPACK_ORDERING_METIS, this tells UMFPACK to use the METIS library to reorder the rows and columns of the matrix for better numerical performance.

The SetOperator() method is then called on the UMFPackSolver object, passing the operator “A” as an argument. This sets the operator for the solver.

Finally, the Mult() method is called on the UMFPackSolver object, passing the right-hand side “B” and the solution “X” as arguments. This solves the linear system and stores the solution in the “X” vector.

In summary, this block of code solves the linear system of equations using different methods depending on the value of the pa variable and the presence of SuiteSparse library, it stores the solution in the “X” vector.

Recover the solution as a finite element grid function

a.RecoverFEMSolution(X, b, x);

This line of code is used to recover the finite element solution from the linear system solution. The RecoverFEMSolution() method is called on the BilinearForm object “a”, passing the linear system solution “X”, the right-hand side “b”, and the GridFunction “x” as arguments.

The RecoverFEMSolution() method is used to project the linear system solution “X” back to the finite element space. This is necessary because the linear system of equations is typically solved in a larger space than the finite element space, due to the imposition of essential boundary conditions. The method takes the solution of the linear system, represented by the vector X, and the linear form b, and returns the solution of the finite element problem, represented by the GridFunction x.

In summary, this line of code is used to project the linear system solution, represented by the vector X, back to the finite element space and store it in the GridFunction x.

Save the refined mesh and the solution

   ofstream mesh_ofs("refined.mesh");
   mesh_ofs.precision(8);
   mesh.Print(mesh_ofs);
   ofstream sol_ofs("sol.gf");
   sol_ofs.precision(8);
   x.Save(sol_ofs);

This output can be viewed later using GLVis: “glvis -m refined.mesh -g sol.gf”.

This code block is used to save the refined mesh and the solution of the finite element problem to files.

An output stream, “mesh_ofs”, is created and opened for the file “refined.mesh” using the ofstream class. The precision of the output stream is set to 8. The Print() method of the Mesh class is then called, passing the output stream “mesh_ofs” as an argument. This method writes the refined mesh to the file in a format that can be read by the MFEM library.

Another output stream, “sol_ofs”, is created and opened for the file “sol.gf” using the ofstream class. The precision of the output stream is set to 8. The Save() method of the GridFunction class is then called, passing the output stream “sol_ofs” as an argument. This method writes the solution of the finite element problem to the file in a format that can be read by the MFEM library.

In summary, this block of code saves the refined mesh and the solution of the finite element problem to files “refined.mesh” and “sol.gf” respectively. These files can be used to visualize the solution in GLVis or other visualization tools that support the MFEM file formats.

Send the solution by socket to a GLVis server

   if (visualization)
   {
      char vishost[] = "localhost";
      int  visport   = 19916;
      socketstream sol_sock(vishost, visport);
      sol_sock.precision(8);
      sol_sock << "solution\n" << mesh << x << flush;
   }

This code block is used to visualize the solution of the finite element problem using GLVis.

The visualization variable is checked to see if it is true. If it is true, a socketstream object, “sol_sock”, is created with the host name “localhost” and the port number 19916. The precision of the socketstream is set to 8.

The “sol_sock” stream is then used to send the solution to GLVis. The “solution” string is written to the stream, followed by the mesh and the solution of the finite element problem. The flush function is then called to ensure that all the data is written to the stream.

This will enable the user to visualize the solution in GLVis by connecting to the specified host and port. The “solution” command tells GLVis that the data that follows is a solution, and the mesh and solution are sent to GLVis to be displayed.

In summary, this block of code sends the refined mesh and the solution to GLVis, if the visualization variable is set to true, so that the user can visualize the solution using GLVis.

Free the used memory

   if (delete_fec)
   {
      delete fec;
   }

This line of code is used to clean up memory allocated by the finite element collection. The delete_fec variable is checked. If it is true, the delete operator is called on the fec pointer, which deallocates the memory that was allocated for the finite element collection.

This ensures that any memory allocated for the finite element collection is properly deallocated and prevents memory leaks.

In summary, this line of code is used to deallocate the memory allocated for the finite element collection, if the delete_fec variable is set to true.

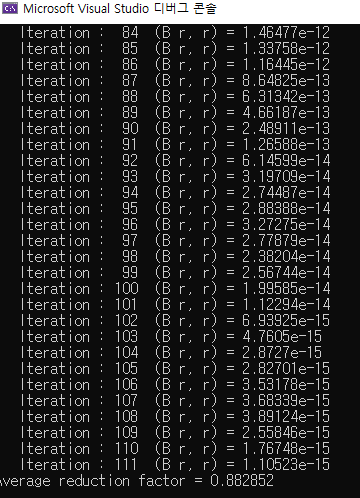
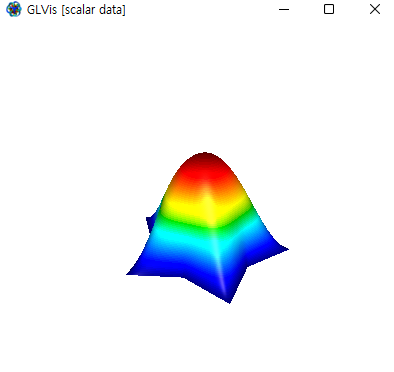
Results