Description

ex0
ex0 -m ../data/fichera.mesh
ex0 -m ../data/square-disc.mesh -o 2

This example code demonstrates the most basic usage of MFEM to define a simple finite element discretization of the Laplace problem

-\Delta u=1

with zero Dirichlet boundary conditions. General 2D/3D mesh files and finite element polynomial degrees can be specified by command line options.

Parse command line options

#include "mfem.hpp"
#include <fstream>
#include <iostream>

This code includes the header files for the MFEM (Modular Finite Element Methods) library, which is a C++ library for solving partial differential equations using the finite element method. The “mfem.hpp” file is the main header file for the library and includes all the necessary headers for using MFEM.

The next two lines include the “fstream” and “iostream” header files. These are part of the standard C++ library and provide input/output functionality for working with files and the console, respectively. The “fstream” header allows for reading from and writing to files, while “iostream” allows for input/output operations with the console.

using namespace std;
using namespace mfem;

These lines use the “using” keyword to bring the “std” and “mfem” namespaces into the current scope. This means that the code in this file will have access to all the functions, classes, and variables defined in the “std” and “mfem” namespaces without needing to prefix them with the namespace name.

The “std” namespace contains a large number of functions and classes that are part of the C++ standard library. The “mfem” namespace contains all the functions, classes, and variables that are part of the MFEM library.

By using the “using” keyword with the “std” and “mfem” namespaces, the code in the file can use the classes, functions and variables from these namespaces without prefixing them with the namespace name. This makes the code more readable and less verbose.

int main(int argc, char *argv[])
{
   const char *mesh_file = "../data/star.mesh";
   int order = 1;
   OptionsParser args(argc, argv);
   args.AddOption(&mesh_file, "-m", "--mesh", "Mesh file to use.");
   args.AddOption(&order, "-o", "--order", "Finite element polynomial degree");
   args.ParseCheck();

This code sets up the command line options for the program. The first line defines a constant character pointer “mesh_file” and assigns the default value “../data/star.mesh” to it. This variable will be used to store the path to the mesh file that the program will use to solve the problem.

The next line defines an integer variable “order” and assigns the default value 1 to it. This variable will be used to store the polynomial degree of the finite element basis functions that the program will use.

The next line creates an instance of the “OptionsParser” class, which is part of MFEM library. The class is used for parsing command-line arguments. The class takes two arguments, the number of arguments passed to the program and the array of arguments passed to the program.

The next three lines use the “AddOption” method of the “OptionsParser” class to add options for the mesh file and the polynomial degree to the program. The first argument passed to the “AddOption” method is the variable to store the value of the option, the second argument is the short form of the option and the third argument is the long form of the option, and the last argument is the help text that will be displayed when the user runs the program with the -h or –help option.

Finally, the “ParseCheck” method is called on the “OptionsParser” class. This method will parse the command line arguments passed to the program and update the values of the “mesh_file” and “order” variables according to the options passed in the command line. If any of the required options are not passed or if there is any error in the command-line arguments, it will also show the error message or the help text.

Read the mesh from the given mesh file, and refine once uniformly.

   Mesh mesh(mesh_file);
   mesh.UniformRefinement();

This code reads the mesh file specified by the “mesh_file” variable and creates an instance of the “Mesh” class from the MFEM library with the read mesh.

The first line creates an instance of the “Mesh” class and initializes it with the mesh file specified in the “mesh_file” variable. The “Mesh” class is one of the fundamental classes in the MFEM library and is used to represent and work with the finite element mesh.

The second line calls the “UniformRefinement” method on the “mesh” object. This method performs uniform refinement on the mesh, which means that it splits each element of the mesh into smaller elements of the same shape. This is done to increase the resolution of the mesh and improve the accuracy of the finite element solution. The number of times the method is called will depend on the desired level of refinement.

Define a finite element space on the mesh. Here we use H1 continuous high-order Lagrange finite elements of the given order.

   H1_FECollection fec(order, mesh.Dimension());
   FiniteElementSpace fespace(&mesh, &fec);
   cout << "Number of unknowns: " << fespace.GetTrueVSize() << endl;

This code sets up the finite element space for the problem.

The first line creates an instance of the “H1_FECollection” class with the polynomial degree specified in the “order” variable and the dimension of the mesh specified by the “mesh.Dimension()” method. The “H1_FECollection” class is a collection of finite element basis functions that are used to represent the solution of the problem. The class is templated on the polynomial degree, and in this case, it is set to the “order” variable.

The second line creates an instance of the “FiniteElementSpace” class, which is another fundamental class in MFEM. It defines the finite element space for the problem. It takes two arguments: a pointer to the mesh and a pointer to the finite element collection. This line creates the finite element space using the mesh and the finite element collection that was created in the previous lines.

The third line prints the number of degrees of freedom in the finite element space. The “GetTrueVSize()” method of the “FiniteElementSpace” class returns the number of degrees of freedom in the finite element space, which is the number of unknowns in the problem. The output of this line is useful for debugging and understanding the size of the problem.

This sets up the basic structure for the finite element method, including the mesh, finite element space, and the finite element collection. The next steps would be to define the problem to solve, set up the linear system, solve the system and post-process the solution.

Extract the list of all the boundary DOFs.

   Array<int> boundary_dofs;
   fespace.GetBoundaryTrueDofs(boundary_dofs);

This code sets up the boundary degrees of freedom for the problem.

The first line creates an instance of the “Array” class from MFEM, and initializes it with an empty array of integers. The “Array” class is a template class that is used to store and manipulate arrays of data.

The second line calls the “GetBoundaryTrueDofs” method on the “fespace” object. This method fills the “boundary_dofs” array with the indices of the true degrees of freedom (DOFs) on the boundary of the mesh.

The true degrees of freedom (DOFs) represent the scalar values that are used to approximate the solution of the problem and are associated with the mesh’s vertices, edges, or faces. In this case, it is getting the boundary true DOFs which are the DOFs that lie on the boundary of the mesh.

This information will be used later in the code to impose essential boundary conditions on the problem, which means that the value of the solution is fixed at certain points on the boundary of the mesh.

Define the solution x as a finite element grid function in fespace.

   GridFunction x(&fespace);
   x = 0.0;

This code sets up and initializes the grid function that will be used to represent the solution of the problem.

The first line creates an instance of the “GridFunction” class and initializes it with a pointer to the finite element space “fespace”. The “GridFunction” class is used to represent the finite element solution of a problem. The class stores the values of the solution at the degrees of freedom of the finite element space.

The second line assigns the value 0.0 to every degree of freedom of the “x” object. The “GridFunction” class overloads the assignment operator, so this line assigns the value 0.0 to every degree of freedom of the finite element space represented by the “x” object. This is used as an initial guess for the solution.

This grid function “x” stores the solution of the problem, it can be used to compute the solution values at any point of the mesh or to extract the solution values at the degrees of freedom for further computation.

Set up the linear form b(.) corresponding to the right-hand side.

  ConstantCoefficient one(1.0);
  LinearForm b(&fespace);
  b.AddDomainIntegrator(new DomainLFIntegrator(one));
  b.Assemble();

This code sets up the right-hand side of the problem.

The first line creates an instance of the “ConstantCoefficient” class, which is a class from the MFEM library that represents a constant coefficient function. The instance is initialized with the value 1.0.

The second line creates an instance of the “LinearForm” class and initializes it with a pointer to the finite element space “fespace”. The “LinearForm” class is used to represent the right-hand side of the weak formulation of the problem. It stores the values of the right-hand side at the degrees of freedom of the finite element space.

The third line calls the “AddDomainIntegrator” method on the “b” object and passes an instance of the “DomainLFIntegrator” class as an argument. The “DomainLFIntegrator” is an abstract class that defines the interface for the domain integrators, which are used to compute the values of the right-hand side at the degrees of freedom. In this case, the constant coefficient one is passed to the integrator.

The last line calls the “Assemble” method on the “b” object. This method assembles the right-hand side of the problem by computing the values of the right-hand side at the degrees of freedom using the domain integrator.

In general, the right-hand side of a problem represents the source term of the differential equation. It is necessary to calculate the right-hand side before solving the equation.

Set up the bilinear form a(.,.) corresponding to the -$\Delta$ operator.

   BilinearForm a(&fespace);
   a.AddDomainIntegrator(new DiffusionIntegrator);
   a.Assemble();

This code sets up the left-hand side of the problem.

The first line creates an instance of the “BilinearForm” class and initializes it with a pointer to the finite element space “fespace”. The “BilinearForm” class is used to represent the left-hand side of the weak formulation of the problem. It stores the values of the bilinear form at the degrees of freedom of the finite element space.

The second line calls the “AddDomainIntegrator” method on the “a” object and passes an instance of the “DiffusionIntegrator” class as an argument. The “DiffusionIntegrator” is an abstract class that defines the interface for the domain integrators, which are used to compute the values of the bilinear form at the degrees of freedom. The specific form of the integrator depends on the problem being solved, in this case the DiffusionIntegrator is used to compute the bilinear form for a diffusion problem.

The last line calls the “Assemble” method on the “a” object. This method assembles the left-hand side of the problem by computing the values of the bilinear form at the degrees of freedom using the domain integrator.

In general, the left-hand side of a problem represents the differential operator of the differential equation. It is necessary to calculate the left-hand side before solving the equation. The bilinear form is also called the stiffness matrix in the case of linear problems.

Form the linear system A X = B. This includes eliminating boundary conditions

   SparseMatrix A;
   Vector B, X;
   a.FormLinearSystem(boundary_dofs, x, b, A, X, B);

This code sets up and solves the linear system of equations that represents the finite element problem.

The first line creates an instance of the “SparseMatrix” class, which is a class from the MFEM library that represents a sparse matrix. The matrix will be used to store the left-hand side of the linear system of equations.

The second line creates an instance of the “Vector” class, which is a class from the MFEM library that represents a vector. The vector will be used to store the right-hand side of the linear system of equations.

The third line creates an instance of the “Vector” class, which is a class from the MFEM library that represents a vector. The vector will be used to store the solution of the linear system of equations.

The fourth line calls the “FormLinearSystem” method on the “a” object, which forms the linear system of equations from the assembled bilinear form “a” , the grid function “x” , the linear form “b” , and the boundary degrees of freedom specified by the “boundary_dofs” array. The method also takes as arguments three output arguments: the sparse matrix “A”, the vector “X” and the vector “B”. The method forms the linear system of equations and stores the resulting matrix A and vectors B and X.

The FormLinearSystem method assembles the stiffness matrix “A” and the right-hand side vector “B” from the bilinear form “a” and linear form “b” using the boundary conditions specified by the “boundary_dofs” array.

The next step would be to solve the linear system A*X = B. This could be done using a direct solver or an iterative solver, depending on the size of the problem and the specific requirements of the application. Once the solution is obtained, it can be stored in the x grid function and post-processed as needed.

Solve the system using PCG with symmetric Gauss-Seidel preconditioner.

   GSSmoother M(A);
   PCG(A, M, B, X, 1, 200, 1e-12, 0.0);

This code solves the linear system of equations using the PCG (Preconditioned Conjugate Gradient) iterative solver method with a Gauss-Seidel smoother (GSSmoother) as a preconditioner.

The first line creates an instance of the “GSSmoother” class, which is a class from the MFEM library that represents a Gauss-Seidel smoother. The smoother is used as a preconditioner for the PCG solver. The Gauss-Seidel smoother is an iterative solver that can be used as a preconditioner to accelerate the convergence of other iterative solvers. The smoother is initialized with the left-hand side matrix “A”.

The second line calls the “PCG” method from the MFEM library, which is an implementation of the Preconditioned Conjugate Gradient (PCG) method for solving symmetric positive definite linear systems. The PCG method takes as input the left-hand side matrix “A”, the preconditioner “M”, the right-hand side vector “B”, the solution vector “X”, the maximum number of iterations “200”, the tolerance “1e-12” and the starting iteration “1”.

The PCG method is an iterative solver that uses the conjugate gradient method to find an approximate solution to the linear system. The method starts with an initial guess for the solution and iteratively improves the solution until it reaches the desired tolerance or the maximum number of iterations. The preconditioner, in this case, the Gauss-Seidel smoother, is used to precondition the system and accelerate the convergence of the method.

The output is the approximate solution of the linear system A*X = B stored in the X vector. The solution is approximate because the iterative solvers usually stop when a certain tolerance is reached.

Recover the solution x as a grid function and save to file.

   a.RecoverFEMSolution(X, b, x);
   x.Save("sol.gf");
   mesh.Save("mesh.mesh");
   return 0; 
 }

This code finalizes the solution process and saves the results.

The first line calls the “RecoverFEMSolution” method on the “a” object. This method takes as input the solution vector “X”, the right-hand side vector “b” and the grid function “x” and recovers the finite element solution from the linear system solution. This is done by updating the values of the grid function “x” at the degrees of freedom of the finite element space using the solution vector “X” and the right-hand side vector “b”.

The second line calls the “Save” method on the “x” object, which saves the grid function “x” to a file named “sol.gf” in MFEM’s native format. This file can be used to visualize the solution or to perform post-processing.

The third line calls the “Save” method on the “mesh” object, which saves the mesh to a file named “mesh.mesh” in MFEM’s native format. This file can be used to visualize the mesh or to perform post-processing.

The final line returns 0, which is the standard convention to indicate that the program has executed successfully.

It is worth noting that the solution process that has been shown is a simplified example, in practice, a more complex problem would require additional steps such as the imposition of boundary conditions, the definition of the problem, and the handling of errors.

Results

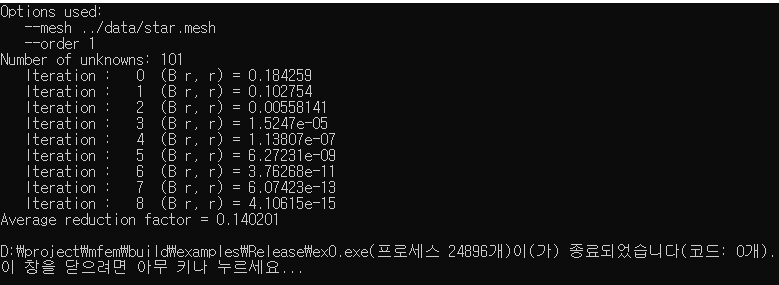
The first line of the output “Number of unknowns: 101” indicates that the finite element problem has 101 degrees of freedom, which is the number of unknowns in the problem.

The rest of the output is generated by the PCG method that is used to solve the linear system of equations. Each iteration of the PCG method is printed in the format “Iteration: n (B r, r) = x” where n is the iteration number, (B r, r) is the inner product of the preconditioned residual vector and the residual vector, and x is the value of the inner product.

The preconditioned residual vector is defined as $B^{-1}r$ where $B$ is the preconditioner and r is the residual vector. The residual vector is defined as $Ax-b$ where $A$ is the left-hand side matrix, x is the solution and b is the right-hand side vector.

The inner product of two vectors is a scalar value that is used to measure the similarity between the vectors. In the case of the PCG method, the inner product of the preconditioned residual vector and the residual vector is used as a measure of the residual error. The goal of the PCG method is to minimize the residual error by iteratively improving the solution.

The output shows that the error decreases with each iteration, and the decrease is exponential. By the 8th iteration, the error is very close to zero which is $10^{-15}$. This means that the solution has reached the desired tolerance and the PCG method has converged.

The last line shows the average reduction factor which is calculated as average of the ratio of the error in each iteration to the error in the previous iteration.

It is worth noting that this output is for one specific problem, the result for other problems could be different. The number of iterations, the error tolerance and the residual error are problem-dependent.