In the ngsolve library, a coefficient function is a function that is used to specify the coefficients of a PDE or boundary condition. Coefficient functions can be either symbolic or numerical.

Symbolic coefficient functions are defined using mathematical expressions and can depend on the coordinates of the domain. They are used to define the weak form of a PDE and are usually used in conjunction with finite element functions to define integrals over the domain.

Numerical coefficient functions are defined using data from a given source, such as a function or an array. They are used to specify the values of the coefficients of a PDE or boundary condition at the degrees of freedom of a finite element function space.

In ngsolve, you can define coefficient functions using the CoefficientFunction constructor. For example:

# define a symbolic coefficient function
f = CoefficientFunction(x*y)

# define a numerical coefficient function
g = CoefficientFunction([1, 2, 3, 4])

After this tutorial you will know how to

1. generate Meshes
2. define a CoefficientFunction,
3. visualize a CoefficientFunction,
4. evaluate CoefficientFunctions at points,
5. print the expression tree of CoefficientFunction,
6. integrate a CoefficientFunction,
7. differentiate a CoefficientFunction,
8. include parameter in CoefficientFunctions,
9. interpolate a CoefficientFunction into a finite element space,
10. define vector-valued CoefficientFunctions, and
11. compile CoefficientFunctions.

from ngsolve import *
from ngsolve.webgui import Draw
from netgen.geom2d import unit_square
import matplotlib.pyplot as plt

1. Generate Meshes

mesh = Mesh (unit_square.GenerateMesh(maxh=0.2))

The mesh object is a finite element mesh that represents the geometry of the domain on which you want to solve a PDE. The Mesh constructor takes in a single argument, which is a mesh object generated from the GenerateMesh method of the unit_square object. The GenerateMesh method discretizes the geometry into a finite element mesh with a maximum element size of maxh.

2. Define a CoefficientFunction,

myfunc = x*(1-x)

The CoefficientFunction class in ngsolve is used to represent mathematical functions that can be used in finite element computations. The myfunc object you created represents the function $f(x) = x*(1-x)$.

You can use this function in a finite element computation by defining it as the coefficient of a PDE, or by using it to specify boundary conditions or initial conditions for a PDE. For example, you might use myfunc as the coefficient of a diffusion equation, or as a Dirichlet boundary condition for a Poisson equation.

You can evaluate myfunc at a given point in the domain by calling it with the coordinates of the point as arguments. For example, to evaluate myfunc at the point $(0.5, 0.5)$, you would use $myfunc(0.5, 0.5)$. This would return the value of myfunc at that point, which is $0.25$.

x is a global variable in Python that represents the current value of the independent variable in a loop. It is often used in for loops to iterate over a sequence of values.

For example, you might use a for loop to iterate over a range of integers, like this:

for x in range(5):
    print(x)

This would output the numbers 0, 1, 2, 3, and 4, because range(5) generates a sequence of integers from 0 to 4.

In the context of finite element computations, x may also refer to the spatial coordinates of a point in the domain. For example, in the code you provided earlier, x is used as the independent variable in the CoefficientFunction myfunc. In this case, x represents the x-coordinate of a point in the domain.

If you are not inside a loop and x is not defined in your code, accessing it will cause a NameError, because x is not a defined variable.

3. Visualize a CoefficientFunction

Draw(myfunc, mesh, "firstfun");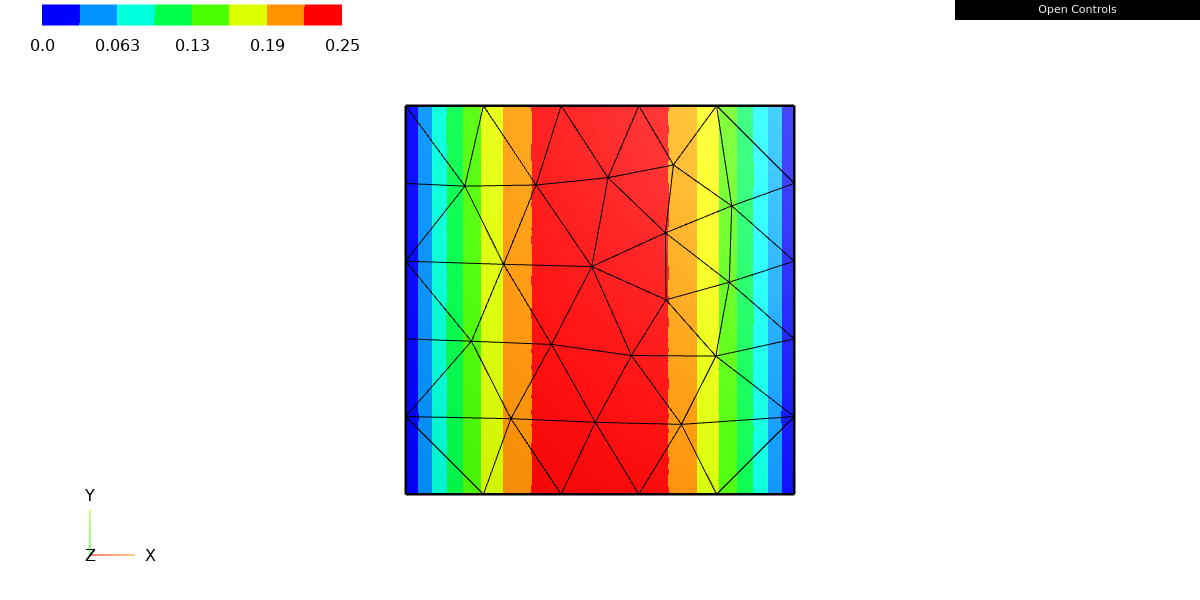

The Draw function from the ngsolve.webgui module can be used to visualize functions defined on a mesh. In this case, the Draw function is being called with three arguments:

• myfunc: the CoefficientFunction to be plotted
• mesh: the Mesh object on which myfunc is defined
• "firstfun": a string specifying the name of the plot

This code will create a plot of myfunc on the specified mesh, using the web-based graphical user interface (GUI) provided by ngsolve. The plot will be given the name “firstfun”.

You can use the Draw function to visualize a variety of different types of data defined on a mesh, including finite element functions, element matrices, and element vectors. You can also specify various options for the plot, such as the range of values to be displayed, the color map to be used, and the type of plot (e.g., surface, contour, or vector field).

To view the plot, you will need to start the ngsolve GUI server and open the plot in a web browser. You can do this by running the Draw.GUI() function in a separate Python session. This will start the GUI server and open a web page in your default browser that allows you to interact with the plots you have created.

4. Evaluate CoefficientFunctions at points

mip = mesh(0.2, 0.2)
myfunc(mip)

# return 
0.16

The mesh object in ngsolve represents a finite element mesh, which is a discrete representation of a continuous domain that is used to solve partial differential equations (PDEs) using the finite element method. The mesh object provides various methods and properties that can be used to access and manipulate the mesh data.

In this code, you are calling the mesh object with two arguments, 0.2 and 0.2. This will return the element (a triangular or quadrilateral element, depending on the type of mesh) that contains the point (0.2, 0.2) in the domain. The resulting element is stored in the mip object.

You can then call the myfunc object with the mip object as an argument, which will evaluate myfunc at the point (0.2, 0.2) within the element mip. The resulting value will be the value of myfunc at that point.

Keep in mind that myfunc is a CoefficientFunction, which is defined on the entire domain, not just on individual elements. Therefore, calling myfunc with an element as an argument will evaluate the function at the coordinates of the element’s center, not at the coordinates of the element’s vertices. If you want to evaluate myfunc at the vertices of the element, you will need to use a different method, such as the Evaluate method of the FiniteElementFunction class.

5. Print the expression tree of CoefficientFunction

pts = [(0.1*i, 0.2) for i in range(10)]
vals = [myfunc(mesh(*p)) for p in pts]
for p,v in zip(pts, vals):
    print("point=(%3.2f,%3.2f), value=%6.5f"
         %(p[0], p[1], v))

This code generates a list of points in the form (x, 0.2), where x ranges from 0 to 0.9 in increments of 0.1. The pts list will contain the following points:

[(0.0, 0.2), (0.1, 0.2), (0.2, 0.2), (0.3, 0.2), (0.4, 0.2),  (0.5, 0.2), (0.6, 0.2), (0.7, 0.2), (0.8, 0.2), (0.9, 0.2)]

The vals list is then created by evaluating myfunc at each of the points in pts using a list comprehension. The resulting values are stored in vals.

Finally, the for loop iterates over the pairs of points and values, and prints a string that includes the coordinates of the point and the value of myfunc at that point. The zip function is used to iterate over the two lists in parallel.

For example, the first iteration of the loop will print the following string:

point=(0.00,0.20), value=0.00000

This code will evaluate myfunc at a series of points along the line y=0.2, and print the coordinates of the points and the values of myfunc at those points. You could modify this code to evaluate myfunc at a different set of points, or to use a different function instead of myfunc.